8. stranica

8. stranica

( Branko Soric: ZNANOST NIJE STATISTICKI DOVOLJNO PROVJERENA - Zagreb, III.- V. 2001.)
---- (DODATAK - E - NASTAVAK)

************

F) Je li moguce ostvariti sistematske dobitke na ruletu?

Ako je rulet potpuno ispravan, kod dugotrajnog kladjenja na tzv. jednostavne sanse (crno, crveno, itd.) treba ocekivati gubitak od oko 1,35% ulozenog novca, i ne postoji nacin da se smanji vjerojatnost gubitka. Medjutim, ako postoji bilo kakva neispravnost ruleta (t.j. "pristranost", engleski: "bias") moguce je, prakticki uvijek, igrati tako da se ocekivani gubitak smanji, a u slucaju velikog bias-a mogao bi se ocekivati i dobitak. Te nacine igre obrazlozio sam u nedovrsenom rukopisu (za knjigu) na engleskom jeziku, ali tu knjigu nisam objavio, jer nisam uspio naci izdavaca u inozemstvu - ne zato sto se tiskanje knjige ne bi isplatilo, nego, cini se, iz nekog drugog razloga. [Napomena: Ne znam koliko izdavaci mozda vode racuna o interesima kockarnicâ? O ruletu se objavljuju mnoge knjige, koje preporucuju razne toboze "uspjesne" sisteme igre, ali time se samo povecava interes igraca za igru, sto zapravo donosi dobitak kockarnicama a ne igracima. Naprotiv, stvarna mogucnost smanjenja ocekivanog gubitka u slucaju "pristranog" ruleta, o kojoj sam ja pisao, mozda ne bi mnogo pomogla igracima (ako "bias" nije velik), ali bi mogla prouzrociti relativno velike gubitke za kockarnice, ukoliko nastoje profitirati pomocu neispravnih ruleta].

Prije vise od deset godina izveo sam formule za izracunavanje kolicinâ serijâ (nizova) crvenih odnosno crnih brojeva, kako kod ispravnog ruleta, tako i kod izmijenjenih vjerojatnosti, te kod oscilirajucih vjerojatnosti sa svim mogucim duljinama fazâ. Neke (jednostavnije) od tih formula objavio sam 1992. godine u knjizici pod naslovom: "Rulet osciliranje vjerojatnosti i mogucnosti dobitka". Medjutim, tamo NISAM objavio KOMPLETNE rezultate proucavanja teorije "pristranog" ruleta. Ta je knjizica bila umnozena u vrlo malom broju primjeraka, i vise se ne moze dobiti; jedan mali dio toga nalazi se ovdje, u nastavku. [To NIJE ona gore spomenuta knjiga na engleskom, koju nisam potpuno dovrsio niti objavio, niti sam ikome pokazao ili poslao taj (neobjavljeni, nedovrseni, PROSIRENI, NADOPUNJENI) rukopis u cijelosti, premda sam DIJELOVE tog rukopisa slao izdavacima].

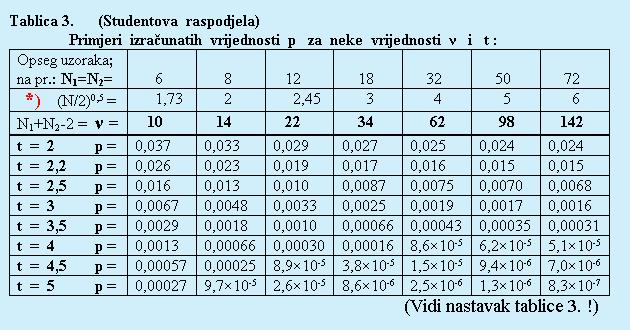
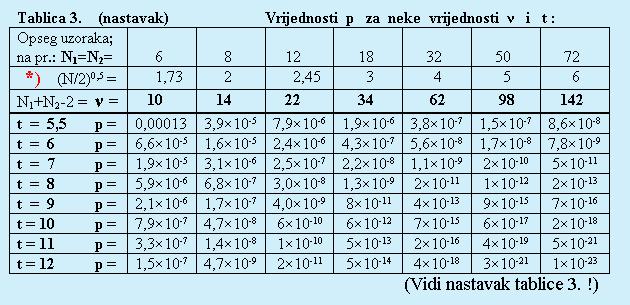
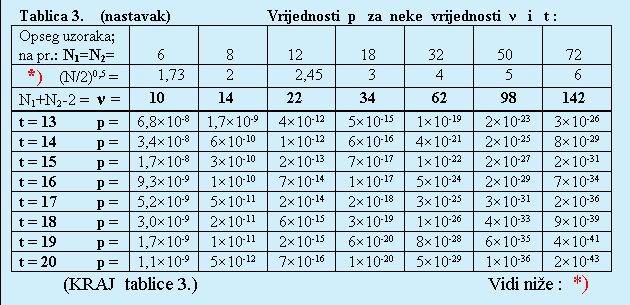
1. Najprije cu navesti neke rezultate, koje je objavio prof. Karl Pearson 1894. godine (u clanku pod naslovom "Science and Monte Carlo"; Fortnightly Review, February 1894).
Evo nekih ocekivanih i opazenih brojeva ogranicenih serija OBJE BOJE (t.j. crvenih i crnih jedinica, dvojki, trojki itd.) u 8178 igara, koje je naveo K. Pearson, a uz njih ovdje navodim i odgovarajuce "amplitude" oscilacijâ vjerojatnosti za duge periode (odnosno duge faze) oscilacijâ, sto sam ih odatle izracunao:
----Ocekivana kolicina = oc.; ------- opazena kolicina = op.;
----"amplituda" oscilacijâ vjerojatnosti = ampl.P ;-- (Ocekivana ampl.P = 0,5/ 0,5)

Jedinicâ se je pojavilo vise nego sto bi se ocekivalo (op.=2462 ; oc.= 2044)
(objasnjenje za to povecanje jedinicâ ne bi bilo bas jednostavno); Dvojki, trojki i
cetvorki bilo je manje nego bi se ocekivalo. Odgovarajuce "amplitude" bile bi ove:
Za dvojke: ampl.P = oko 0,6/ 0,4 ; ------ za trojke: ampl.P > 0,7/ 0,3 ;
za cetvorke: ampl.P > 0,6/ 0,4 ; DULJIH serija bilo je VISE od ocekivanja:
--- petice:...........oc.=128 ;.....op.=135 (visak) ;...ampl.P>0,7/ 0,3
--- sestice:...... ...oc...=64 ;.....op..=81 (visak) ;....ampl.P>0,6/ 0,4
--- sedmice:........oc...=32 ;.....op..=43 (visak) ;....ampl.P>0,6/ 0,4
--- osmice:..........oc..=16 ;......op..=30 (visak) ;....ampl.P>0,6/ 0,4
--- devetice:........oc.....=8 ;.....op..=12 (visak) ;....ampl.P>0,55/ 0,45
--- desetice:.........oc....=4 ;......op...=7 (visak) ;....ampl.P>0,55/ 0,45
--- jedanaestice:..oc....=2 ;......op...=5 (visak) ;....ampl.P>0,6/ 0,4

2. Kolicine crvenih (Rn) i crnih (Bn) ogranicenih serija za duge, simetricne faze oscilacijâ vjerojatnosti mogu se izracunati po slijedecoj formuli:

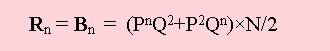
gdje su P i Q vjerojatnosti crvenih odnosno crnih brojeva (na pr. P=Q=0,5 ; ili: P=0,6 Q=0,4 ; itd.; P+Q=1); n je duljina serije (na pr. n = 1, 2, 3, itd., za jedinice, dvojke, trojke itd.); N je odredjeni veliki broj igara.

3. Kod sistema Martingale ulog se podvostrucuje nakon gubitka. Pretpostavimo, da se kladimo na crveno (t.j. u svakoj igri stavljamo ulog na crveno) te da podvostrucujemo ulog "do crne trojke"; to znaci (ako pocetni ulog oznacimo brojem 1) da nakon prvog crnog broja ulazemo 2, nakon drugog uzastopnog crnog broja ulazemo 4, a nakon treceg uzastopnog crnog broja prestajemo podvostrucivati te ulazemo ponovno 1 t.j. pocetni ulog. Nakon svake crne trojke izgubili smo 1+2+4 = 7, ali buduci da se crna sestica sastoji od dvije crne trojke, na svaku crnu sesticu gubimo 2×7=14, na svaku crnu deveticu gubimo 3×7=21 itd. Da bismo mogli izracunati koliko cemo novca ukupno izgubiti u velikom broju igara (N), moramo najprije izracunati "totalni broj" crnih trojki u N igara.
Totalni broj crvenih odnosno crnih serija odredjene duljine (Rnt odnosno Bnt) kod dugih simetricnih faza oscilacijâ vjerojatnosti mozemo izracunati po slijedecoj formuli:

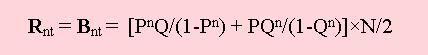
Na pr., ako je P=0,6 i Q=0,4 (ili obratno) totalni broj crnih trojki u 1000 igara iznosi
[0,6^3×0,4/(1-0,6^3) + 0,6×0,4^3/(1-0,4^3)]×500 = 75,615 = B3t a ukupni gubitak je B3t×(-7) = -529,31. (Ako je P=Q=0,5 tada je B3t = 71,429....... B3t×(-7) = -500).
U 1000 igara u prosjeku se pojavi 500 crvenih brojeva (kod simetricnih oscilacija). Kod sistema Martingale dobiva se 1 na svaki crveni broj, dakle ukupni dobitak u 1000 igara iznosi +500, a "cisti gubitak" (u nasem primjeru) je +500-529,31 = -29,31 u 1000 igara (u prosjeku). Tome jos treba dodati GUBITKE NA NULU! Medjutim, ako igramo po "obrnutom Martingaleu", t.j. ako podvostrucujemo ulog nakon DOBITAKA, "cisti gubitak" se pretvara u "cisti dobitak" od +29,31 na 1000 igara, ali od toga treba odbiti gubitke na nulu. (Ako je P=Q=0,5 nema "cistog" dobitka ni gubitka jer je 500-500=0, ali postoje gubitci na nulu).
Ovdje necemo ulaziti u ostale probleme, niti u nacin izracunavanja ukupnih uloga, gubitaka na nulu, itd. Navodim samo slijedeci primjer:
Pretpostavimo da je, kod simetricnih oscilacija vjerojatnosti sa dugim fazama, P=0,6 Q=0,4 (odnosno obratno u suprotnoj fazi), te da ulazemo na CRVENO i podvostrucujemo do CRVENE sestice (OBRNUTI Martingale). Totalni broj crvenih sestica u 1000 igara (u prosjeku) iznosi 11,022 ; Na svaku crvenu sesticu dobivamo 1+2+4+8+16+32 = +63 a na crne brojeve gubimo ukupno -500. Gubitak na nulu u 1000 igara iznosi u ovom slucaju (prosjecno) -43 na 1000 igara.
Cisti prosjecni dobitak je 11,022×63 -500 -43 = +151,4 u 1000 igara.

Ako su faze oscilacija krace, cisti dobitak postaje manji. (Izracunavanje je u tom slucaju daleko kompliciranije). Takodjer se cisti dobitak smanjuje u slucaju manjih amplituda oscilacijâ vjerojatnosti. Ipak, igrac moze prakticki uvijek preokrenuti eventualnu neispravnost ruleta ("pristranost", "bias") u svoju korist - premda ta korist ne mora biti velika! (Kod malih amplituda mogao bi se samo donekle umanjiti neizbjezni gubitak na nulu!) Ako je rulet potpuno ispravan, t.j. ako je uvijek P=Q=0,5 , neizbjezno se gubi (u prosjeku, pri dovoljno dugom igranju) 1,35% svega ULOZENOG novca (na ruletu kakav se igra u Monte Carlu, te ako se ulaze na crveno, odnosno na crno, par, nepar, passe ili manque).

Postoje, dakle, nacini (sistemi) igre koje je prakticki uvijek dobro primijeniti, ne vodeci racuna o tome je li rulet ispravan ili nije (je li P=Q, ili je P>Q, ili P<Q). Takav nacin igre, u slucaju da je rulet ispravan, nije losiji od bilo kojeg drugog nacina, ali je u slucaju neispravnosti ruleta (bias-a) povoljniji za igraca jer smanjuje prosjecne, "ocekivane" gubitke, odnosno gubitke u vrlo velikom broju igara; to znaci slijedece: kad bi igraci mogli odigrati neizmjerno velik broj igara, oni bi, u slucaju potpuno ISPRAVNOG ruleta, u prosjeku pretrpili gubitke (jer se ne mogu izbjeci gubitci na nulu), a u slucaju NEISPRAVNOG ruleta ti bi gubitci bili manji, ali nije sigurno KOLIKO bi bili manji, a jos je manje sigurno da li bi se umjesto tih smanjenih gubitaka pojavili dobitci.
U vrlo velikom broju igara igrac nikada ne moze biti siguran da ce ostvariti konacni, ukupni, cisti dobitak (jer bias ne mora biti velik) - dok kockarnica, naprotiv, moze (ako hoce) ostvariti prakticki sigurne dobitke (t.j. ako pazi da rulet bude ispravan).

Prema K. Pearsonu, rulet u Monte Carlu NIJE MOGAO BITI ISPRAVAN, ali to je bilo 1894. godine! Ako su tada postojale simetricne oscilacije vjerojatnosti sa visokim amplitudama (P/Q = 0,6/0,4 odnosno 0,4/0,6), DANAS TO VISE NE MORA BITI TAKO!
************
K R A J

Statisticko zakljucivanje