|
|
( Branko Soric: ZNANOST NIJE STATISTICKI DOVOLJNO PROVJERENA
- Zagreb, III.- V. 2001.)
-----III. DIO |
 |
|
7. Zablude nekih strucnjaka
Mnogi kazu, da su neke
znanosti (medicina, psihologija, i dr.) jednim dijelom "statisticki provjerene". To, navodno, znaci da mozemo biti prilicno
sigurni u istinitost tako provjerenih znanstvenih tvrdnji - sto je u ovom trenutku, nazalost, vrlo krivo uvjerenje! Pri tome
se nerijetko krivo zamislja, da vjerojatnost ne-istinosti neke "provjerene" tvrdnje otprilike odgovara postignutoj razini
statisticke znacajnosti (p<¤=alfa). Dakle, ako se u nekom pokusu postigne vrijednost p<0,01, sto znaci da je rezultat
statisticki znacajan na razini od 1% (¤=alfa = 0,01), cesto se smatra da mozemo biti 99% sigurni u istinitost dobivenog rezultata
("otkrica").
U nekim udzbenicima kaze se, otprilike, da je "razina znacajnosti rizik koji preuzimamo kad tvrdimo da
je nesto statisticki znacajno, t.j. da nije slucajno", odnosno da razlika dobivena na uzorcima (na pr. razlika aritmetickih
sredina), koja je statisticki znacajna "na razini rizika od 5%", znaci "da postoji samo 5% sanse" da nema razlike medju aritmetickim
sredinama obiju populacija. Ocito, pod tim "rizikom" i "sansom" misli se na vjerojatnost laznog (pogresnog) otkrica nekog
efekta koji zapravo ne postoji.
Sto znaci ta gore spomenuta "vjerojatnost da je OTKRICE POGRESNO" (t.j. "sansa da zapravo
nema razlike")?
Vjerojatnost bilo kojeg dogadjaja jednaka je proporciji (ili postotku) takvih dogadjaja u vrlo velikom
skupu odgovarajucih pokusaja. Iz samog gornjeg pitanja se vidi da se to pitanje odnosi na vjerojatnost POGRESNOG zakljucka
(t.j. laznog "otkrica") u skupu ucinjenih OTKRICA, t.j. misli se na proporciju laznih otkrica u vrlo velikom skupu ucinjenih
otkrica. Ako taj vrlo veliki skup ucinjenih otkrica oznacimo slovom r , a skup laznih otkrica je ¤a (=alfa×a), onda spomenuta
proporcija (koja je jednaka vjerojatnosti da je otkrice pogresno) iznosi: ¤a/r . S druge strane, ocito, pod vjerojatnoscu
("rizikom", "sansom") od 5% podrazumijeva se vjerojatnost znacajnosti "¤=alfa = 5%", za koju se u svim udzbenicima statistike
objasnjava da je to (pri toj odabranoj razini znacajnosti) vjerojatnost dobivanja znacajnog rezultata (t.j. "otkrica") u vrlo
velikom skupu (znanstvenih) POKUSA U KOJIMA JE ISTINITA NUL-HIPOTEZA, a to znaci da u svim tim pokusima NEMA razlike medju
populacijma. (Napomena: Kao sto je receno, uciniti "otkrice" razlike medju populacijama znaci odbaciti nul-hipotezu).
Nadam
se da ce se svatko sloziti, da je velika razlika izmedju pojma "proporcija laznih otkrica MEDJU UCINJENIM OTKRICIMA" (= ¤a/r)
i pojma "proporcija laznih otkrica U ONIM POKUSIMA u kojima zapravo ne postoji pretpostavljeni efekt t.j. U KOJIMA NEMA PRETPOSTAVLJENE
RAZLIKE MEDJU POPULACIJAMA" (=¤a/a =¤). (Vidi sliku 1. u I. dijelu). Pa ipak, u knjigama se nerijetko nalaze krive tvrdnje!
Kako je to moguce?
Problem nije samo u vecoj ili manjoj sposobnosti shvacanja, nego, na zalost; i u osobnim interesima
pojedinih znanstvenih istrazivaca (medju koje spadaju, na pr., i neki lijecnici) kao i statisticarā. Mnogi od njih, naime,
zele na sto brzi i sto laksi nacin doci do eksperimentalnih rezultata koje ce moci objaviti kao "provjerena" znanstvena otkrica,
a neki mozda taj svoj cilj stavljaju cak iznad opceg cilja da znanost mora biti istinita. (Istinita znanost moze biti samo
ona, koja sadrzi, ako ne 100% istinitih tvrdnji, a onda bar BLIZU 100% - na pr. 99% ili bar 95%; premda bi se moglo prigovoriti
i posumnjati nije li previse i 1% neistine u znanosti, a kamoli 5%!).
[Usput, kad sam vec spomenuo svoje kolege lijecnike,
jedna DIGRESIJA: Moram priznati onim citateljima, koji imaju najbolje misljenje o SVIM lijecnicima (bez izuzetka), da NE ZNAM
odgovor na slijedeca pitanja: (1) Lijecnici se nerijetko trude da pod svaku cijenu, pa i najkompliciranijim operacijama, sto
dulje odrze na zivotu cak i najteze i najbeznadnije pacijente. Da li SVI oni to rade (a) ZBOG ZELJE PACIJENATA (koji su, doduse,
ponekad zavarani obecanjima o vecoj uspjesnosti lijecenja nego sto je stvarno moguca), ili se mozda U NEKIM SLUCAJEVIMA radi
(b) o ZELJI SAMIH LIJECNIKA za povecanjem svog ugleda, za isticanjem svojih strucnih sposobnosti, za vecom zaradom, itd.?
(Na pr., dogadjalo se ponekad, da su takvi teski bolesnici bili prisiljeni pristati na mutilirajucu operaciju, zbog upozorenja
da ce, u protivnom slucaju, umrijeti u teskim mukama i bolovima. Nije mi poznat ni jedan konkretan slucaj u kojem bi na takvom
teskom pacijentu bila izvrsena kordotomija). (2) Neki lijecnici traze sto vise raspolozivih organa za transplantacije. Jeste
li od tih istih lijecnika culi, da jednako cesto i jednako glasno traze najstroze ogranicavanje prometa (automobilskog i drugog)
t.j. zabranu voznje (ako nije neophodno potrebna), cime bi se bez sumnje SMANJIO BROJ POGINULIH u prometnim nesrecama, ali
bi se, jasno, smanjila i opskrba organima potrebnim za transplantacije?!]
Najveci problem je mozda taj, sto NE MOZEMO
BITI SIGURNI NI U ISTINITOST PRIKUPLJENIH STATISTICKIH PODATAKA (koji se kasnije statisticki obradjuju). Ne dogadja se bas
rijetko, da se svjesno ili nesvjesno rabe neistiniti ili "nategnuti" podatci, pa se na taj nacin lako postizu nova "otkrica".
(U novinama se gotovo svakodnevno moze citati kako su znanstvenici nesto "dokazali" - a sutra se mozda vec "dokaze" suprotno!).
Ali, i kod onih strucnjaka, koji iskreno zele biti potpuno objektivni, nisu rijetke razne zablude. Evo par primjera:
U jednoj knjizi (vidi nize u popisu literature: Vrhovac B., 1984.) pise slijedece: "Zbog varijabilnosti pojedinacnih podataka
u rezultatima pokusa valja ih svakako statisticki analizirati. Pokusi bez takve analize rezultata nisu adekvatni. Uz svaki
rezultat mora biti navedena mjera za njegovu statisticku pouzdanost, t.j. naznaka VJEROJATNOSTI DA NIJE SLUCAJAN." (Podcrtao
B.S.).
PRIMJEDBA: (Svaka vjerojatnost je jednaka proporciji u vrlo velikom skupu). Sto znaci ta upravo spomenuta "vjerojatnost
da NALAZ NIJE SLUCAJAN"? Iz samog tog izraza jasno je da se misli na postotak (proporciju) NE-SLUCAJNIH nalaza u vrlo velikom
skupu NALAZA. Ocito, "slucajnim nalazom" se smatra "lazni nalaz" ("lazno otkrice") t.j. nalaz neke razlike na uzorcima, premda
ta razlika zapravo ne postoji medju populacijama. Dakle, ponovimo jos jednom: "Vjerojatnost da nalaz nije slucajan" znaci
proporciju ne-slucajnih nalaza (t.j. ISTINITIH otkrica) u velikom skupu nalaza (OTKRICA). Autor trazi da se ta vjerojatnost
naznaci uz rezultat pokusa, ne uvidjajuci da ono sto se moze navesti - a to je postignuta razina statisticke znacajnosti (na
pr. p < 0,05 = ¤=alfa ili 1-p > 0,95 = 1-¤) - uopce NIJE ta vjerojatnost (odnosno gore spomenuta proporcija)! Naprotiv,
vjerojatnost znacajnosti (¤=alfa) jednaka je proporciji (laznih) otkrica u velikom skupu pokusa u kojima nema razlike medju
populacijama - a to je nesto sasvim razlicito od vjerojatnosti da dobiveni razultat nije (ili da jest) lazan! Evo jos kraceg
objasnjenja:
Vrlo velik broj nezavisnih pokusa oznacili smo slovom n. Medju njima, vrlo veliki broj pokusa bez razlike
medju populacijama je a. Prema tome, broj pokusa u kojima postoji razlika je n-a = b (pretpostavljamo da je i taj broj vrlo
velik). Odatle proizlazi, da broj laznih otkrica iznosi:
¤a = a', dok je broj istinitih otkrica fb = b', (gdje je f ima
neku vrijednost manju od 1). Vjerojatnost "da nalaz nije slucajan", t.j. vjerojatnost (proporcija, postotak) istinitih otkrica,
je
b'/(a'+b') = fb/(¤a+fb), sto je, ocito, sasvim razlicito od ¤ odnosno 1-¤.
U istoj knjizi (str. 28.) pise:
"Rezultat je u pravilu statisticki signifikantan vec uz 95% sigurnosti da nije slucajan. No preostalih 5% jest vjerojatnost
drugacijih rezultata, a to je na velikoj populaciji prilicno mnogo."
PRIMJEDBA: To takodjer pokazuje da se statisticka
signifikantnost od 5% krivo poistovjecuje sa vjerojatnoscu da je rezultat "slucajan" (lazno otkrice); t.j. krivo se ocekuje
5% laznih otkrica medju svim ucinjenim otkricima.
(U istoj knjizi, str. 65.:) ".... drzat cemo da razlike izmedju
dvaju lijecenja nema dok se ne dokaze suprotno. Suprotno se, medjutim, ne moze nikada dokazati; moze se samo reci s ODREDJENOM
VJEROJATNOSCU ("probability" ili P) da su rezultati koje smo dobili uistinu posljedica RAZLICITOSTI dvaju nacina lijecenja
...." (Podcrtao B.S.)
PRIMJEDBA: Krivo se misli, da je vjerojatnost istinitog otkrica "odredjena" t.j da je poznata iz
same postignute razine znacajnosti!
(U istoj knjizi, str. 66.; podcrtao B.S.:) "Pretpostavimo da u dvije skupine imamo
po 30 bolesnika. U jednoj se lijecenjem A izlijeci 80%, a u drugoj lijecenjem B 40% ispitanika. Cini nam se da postoji razlika,
statistickom analizom dobijemo P<0,01 i zakljucujemo DA JE VRLO VJEROJATNO DA ZAISTA POSTOJI RAZLIKA izmedju tih dvaju
lijecenja". (......) "... ali mozemo se upitati da li bi razlika u lijecenju uistinu bila 40%?" (......) "...zelimo saznati
s 95% pouzdanosti (100% sigurnost ne postoji!) kolika je zbiljska razlika izmedju ta dva lijecenja. Taj se raspon naziva granicama
pouzdanosti..." (......) "Za nas primjer dvije standardne pogreske razlike iznose 23% pa mozemo zakljuciti DA JE 95% VJEROJATNO
DA JE NOVO LIJECENJE BOLJE OD STAROGA IZMEDJU 17% i 63% (40 ± 23). Dakle, ako klinicar pocne svojim bolesnicima davati novi
lijek, terapijski ce dobitak biti izmedju 17% i 63%. Ta je informacija znatno prakticnija nego samo sturi podatak od 40% (P<0,01)...".
PRIMJEDBA:
RADI SE O UOBICAJENIM, VRLO RASIRENIM KRIVIM SHVACANJIMA (za koja ne treba "okrivljavati" autore citirane
kjnige!)
Ako je P<0,01=¤=alfa odnosno 1-P>0,99=1-¤, tada 0,99 NIJE vjerojatnost postojanja razlike medju populacijama
u slucaju kad smo dobili takav znacajan rezultat u nasem ispitivanju. Drugim rijecima, 0,99=1-¤ NIJE proporcija ISTINITIH
razlika (istinitih otkrica) u vrlo velikom skupu rezultata (otkricā) ZNACAJNIH na razini 0,01.
Osim toga, "granice
pouzdanosti od 95%" NE ZNACE da ce 95% pravih (istinitih, VECIH OD NULE) razlika medju populacijama biti unutar tih granica!
Naime, ako je razlika medju populacijama jednaka nuli, onda nam nista ne vrijede granice koje obuhvacaju nulu, jer se u tom
slucaju ne radi o otkricu nego o promasaju, koji, jasno, ne ulazi u znanost; a nama je vazan postotak (proporcija) istine
U ZNANOSTI! Dakle, zanimanju nas granice pouzdanosti koje su izracunate u velikom broju OTKRICA, a one lako mogu - u danasnjoj
situaciji, kad se ne zna omjer r/n - obuhvacati mnogo manje od 95% pravih razlika (mozda 90%, mozda 70%, mozda jos mnogo manje);
prema tome, proporcija (odnosno postotak) pogresaka lako moze biti mnogo veca od 0,05 (odnosno od 5%). Ta proporcija pogresnih
ocjena efekta u skupu otkricā (koju cemo ovdje oznaciti slovom E) veca je od vrijednosti Qmax izracunate po formuli (1) (vidi
gore formulu (1)!), t.j.: E=¤n/r >Qmax (kao sto je objasnjeno u ranijem radu: Soric, 1989; vidi nize u popisu literature).
|
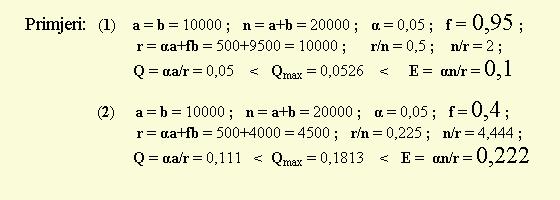
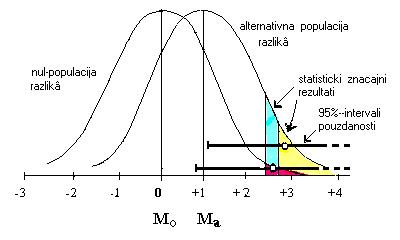
Gornja slika i slijedeci primjer pokazuje, kako je moguce pogrijesiti
i kod primjene 95-postotnih (na pr. jednostranih) intervala pouzdanosti na rezultate znacajne na razini alfa=0,01:
Pretpostavimo
da je: a = b = 10000 ; __ n = 20000 ; __ alfa = 0,01
Radi jednostavnijeg racunanja, uzmimo da su u svim pokusima jednaki
opsezi dvaju uzoraka: N1 = N2 = 30 (dakle, postoji Studentova raspodjela sa N1+N2-2 = 58 stupnjeva slobode), te da u svim
pokusima u skupu b razlika aritmetickih sredina (efekt) iznosi jednu standardnu gresku (= 1 s.g.).
Tada je: f = 0,0846
; ___ ¤a (=alfa×a) = 100 ; ___ fb = 846
r = ¤a+fb = 946 ; __ Q = 100/946 = 0,106 ; __ Qmax = 0,203
Broj pogresnih
procjena efekta pomocu jednostranih 95-postotnih intervala pouzdanosti, u skupu (r) otkricā (t.j. rezultatā znacajnih na razini
¤=0,01), iznosi: 0,01×a + 0,05×b = 100+500 = 600 odnosno u postotcima: 600/946 = 0,634 = 63,4%.
(Ako bismo uzeli mnogo
vece uzorke, raspodjela bi bila slicna normalnoj, a postotak pogresnih procjena bi iznosio priblizno 59%).
Slicnih
primjera pogresnog shvacanja moglo bi se naci mnogo. Neki autori (statisticari i drugi) shvacaju pogresku, ali (koliko mi
je poznato) u knjigama se za sada ne navodi i ne objasnjava ispravni nacin statistickog provjeravanja hipoteza i zakljucivanja.
Razlog za to, U NEKIM SLUCAJEVIMA, moze biti (kao sto je gore spomenuto) osobni interes. Naime, osobni interes nekih
statisticarā moze se podudarati sa interesom istrazivacā kao korisnika njihovih usluga i knjiga. Prije objavljivanja nekih
mojih clanaka (na pr., v. nize u popisu lit.: Soric B. 1981.) recenzenti nekih uglednijih znanstvenih casopisa (i to onih
casopisa, koji upravo objavljuju nedovoljno provjerene rezultate!!) davali su dvije vrste medjusobno SUPROTNIH misljenja:
Jedni su tvrdili da ja nisam u pravu, da su uobicajene razine znacajnosti sasvim zadovoljavajuce, te da zato NIJE POTREBNO
OBJAVITI moje tekstove. Drugi su, naprotiv, izjavljivali da sam ja potpuno u pravu, ali da je to sve "samo po sebi jasno"
i trivijalno, te da zato (OPET) - NIJE POTREBNO OBJAVITI moje tekstove. OVIM POTONJIMA, OCITO, NIJE SMETALO TO, STO SE TE
"TRIVIJALNE" ISTINE ILI NE ZNAJU ILI SE VISE-MANJE IGNORIRAJU U UDZBENICIMA I U PRAKSI! (Napomena: Spomenuti i drugi moji
tekstovi kasnije su ipak bili objavljeni).
Cini mi se, da neki strucnjaci mozda ipak dovoljno ne shvacaju, sto bi
zapravo trebalo napisati i objasniti u svakom udzbeniku statistike, A TO JE SLIJEDECE:
KRIVO JE (BAR U DANASNJOJ SITUACIJI)
ODBACITI NUL-HIPOTEZU,
U POJEDINACNOM POKUSU, NA TEMELJU RELATIVNO NISKE RAZINE
STATISTICKE ZNACAJNOSTI (NA PR. 5%,
A MOZDA I 1%)!
To je krivo zato, sto je pri tome (danas) RIZIK NEPOZNAT (za razliku od onoga
sto pise u udzbenicima!).
Ispravniji postupak bio bi ovaj:
----- Ili treba (1) voditi racuna o broju (r) dobivenih znacajnih rezultata
("otkrica")
u poznatom velikom broju (n) pokusā, pa odatle (priblizno)
izracunati maksimalni postotak laznih otkrica medju svim ucinjenim
otkricima (Qmax),
----- ili treba (2) odbaciti nul-hipotezu u pojedinacnom pokusu samo onda,
kada se postigne
mnogo visa razina znacajnosti nego sto je danas uobicajeno
t.j. znatno manja vrijednost p , na pr. blizu 0,000 000 001
= 10^-9 ili (mozda)
bar p< 0,000 001 = 10^-6 (premda NIJE ISKLJUCENO, da bi se nul-hipoteze
mozda mogle odbaciti
u pojedinacnim pokusima i na temelju neke druge
vrijednosti p - recimo p<0,0001 (?) ili p<0,001 (??) ALI TO BI TEK
TREBALO
DOKAZATI!)
[O gornjemu (sto je navedeno pod (1) itd.) pisao sam 1981. do 1989. godine (vidi nize: popis literature,
Soric B., 1981., 1989.). O neispravnom shvacanju znacenja i vrijednosti (korisnosti) statisticke znacajnosti pisali su i drugi
autori (na pr.: Iyengar S. i Greenhouse J. B. 1988; Morrison D. E. i Henkel R. E 1973; Oakes M.W. 1986; Soric B. i Petz B.
1987.; vidi nize: popis lit.)].
Kako bi, dakle, trebali postupati istrazivaci? Nije lose objaviti rezultate sa postignutim
vrijednostima p oko 0,05 do 0,001 (ili sl.), ali ne treba ih smatrati dovoljno provjerenim otkricima, nego samo "prijedlozima"
za daljnje provjeravanje (dok se eventualno ne utvrdi koja razina znacajnosti je zapravo dovoljna za pojedinacne pokuse).
Ako je alternativna hipoteza zaista ispravna, ponavljanjem takvih POJEDINACNIH pokusa NA VECIM UZORCIMA lako ce se postici
mnogo vise razine znacajnosti;
ILI, mogu se ponavljati dovoljno veliki SKUPOVI takvih pokusa radi postizanja dovoljno
male proporcije Qmax (eventualno cak uz vrlo niske razine znacajnosti, kao na pr. p = 0,05 ili p = 0,1 ili 0,2 itd.).
Bez
ponavljanja ne mogu se smatrati istinitim otkricima cak ni oni rezultati, kod kojih su postignute ekstremno visoke razine
statisticke znacajnosti, jer se moze raditi o (nenamjernim) sistematskim pogreskama u prikupljanju podataka (ili o drugim
neispravnostima).
************
------- GORE SPOMENUTA LITERATURA:
Vrhovac B., i dr.: Klinicko ispitivanje
lijekova, Skolska knjiga, Zagreb, 1984.
------------ (str.27-28., 65.)
Iyengar S. and Greenhouse J. B.: "Selection
Models and the File Drawer Problem",
-------------- Statistical Science, 3, 1988 (str. 109-135.)
Morrison D. E. and
Henkel R. E. (eds.): The Significance Test Controversy (2nd ed.),
-------------- Aldine, Chicago, 1973
Oakes M. W.:
Statistical Inference: A Commentary for the Social and Behavioural
-------------- Sciences, John Wiley, 1986, New York
Soric B.: "Poboljsanje metode i kontrola ispravnosti statistickog odlucivanja",
-------------- Zdravstvo, 23, 1981.
(str. 154-170.)
Soric B. i Petz B.: "Koliki postotak znanstvenih otkrica nisu otkrica?", Arhiv za
-------------- higijenu
rada i toksikologiju, 38, 1987. (str. 251-260.)
Soric B.: "Statisitcal 'Discoveries' and Effect-size Estimation", Journal
of the
-------------- American Statistical Association, Vol. 84, no. 406 (Theory and Methods), 1989
----------- (str.
608-610.)
************
(NASTAVAK JE NA 5. STRANICI)
5. stranica
|

