5. stranica

( Branko Soric: ZNANOST NIJE STATISTICKI DOVOLJNO PROVJERENA - Zagreb, III.- V. 2001.)
--- DODATAK
A) --- Ad 4.1 --- ("Slucaj vrlo velikih skupova")
--------Potpuni izvod formule (1)

U ranijem radu (Soric B., 1989.) izvedena je formula za proporciju laznih otkrica (Q):
Q = [(n/r)-(1/f)]/[(1/¤)-(1/f)] ; ---- (gdje je ¤=alfa); ---- odatle se dobiva najveca vrijednost Q = Qmax (uvrstavanjem najvece vrijednosti f = 1) odnosno najmanja vrijednost Q = 0 (uvrstavanjem najmanje vrijednosti f = r/n).
Ovdje cemo izvesti formulu za Qmax na drugi nacin:

Polazimo od pretpostavke da je, u najgorem slucaju, a = n, t.j. da su sve nul-hipoteze istinite. U tom slucaju iz svih n pokusa dobili bismo ¤n (=alfa×n) laznih otkrica. Ukupni broj otkrica je r (on nam je poznat, jer mozemo izbrojiti sva ucinjena otkrica). Ako od toga broja r odbijemo lazna otkrica (¤n), dobijemo broj istinitih otkrica:
fb = r-¤n .

Kad smo na taj nacin saznali da postoji najmanje r-¤n istinitih otkrica, tada znamo da i u skupu n mora biti bar isto toliko istinith alternativnih hipoteza. Dakle, sad znamo da nisu sve nul-hipoteze istinite (kao sto smo pretpostavili na pocetku), nego njihov najveci broj iznosi:
a(privremena vrijednost) = n-(r-¤n) = n-r+¤n. Odatle (mnozenjem sa ¤) dobivamo
¤a = ¤n-¤r+¤¤n laznih otkrica --- (gdje je ¤¤ = alfa na kvadrat).
Sad nalazimo i drugaciji broj istinitih otkrica:
fb = r-¤n+¤r-¤¤n ------ (¤¤ = alfa na kvadrat).

Taj broj istinitih otkrica opet odbijemo od n pa dobijemo novi broj istinitih nul-hipoteza:
a = n-r+¤n-¤r+¤¤n , iz kojega dobijemo novi najveci broj laznih otkrica (novi ¤a), itd., itd. (teoretski: u beskonacnost). Na taj nacin dobivamo da najveci broj laznih otkrica iznosi:

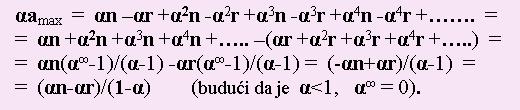
Najvecu proporciju laznih otkrica u skupu svih otkrica (r) dobijemo dijeljenjem sa r (pri cemu cemo takodjer brojnik i nazivnik podijeliti sa alfa), t.j.:

Qmax = ¤(a,max)/r = [(n/r)-1]/[(1/¤)-1)] ........(1)
(gdje je ¤=alfa)

Ta formula bi tocno vrijedila za neizmjerno velike skupove pokusa, a kod skupova od nekoliko tisuca pokusa ona daje samo pribliznu vrijednost Qmax . [Za takve (ne jako velike) skupove mozemo dosta tocno odrediti prakticki najvecu mogucu vrijednost Qmax na nacin koji je prikazan pod 4.2.]

************

B) --- Ad 4.3 --("Koliko je korisno znati vrijednost Qmax ?")

Ako je Qmax velik, stvarna vrijednost Q moze biti mnogo manja, ali je u tom slucaju i prosjecni efekt mnogo manji. (To vrijedi uz pretpostavku da se skup n sastoji od podskupa (a) istinitih nul-hipoteza i od podskupa (b) istinitih alternativnih hipoteza). Zato je korisno izracunati Qmax za VELIKI SKUP otkrica, te je pozeljno postici sto manju vrijednost Qmax . Ako nemamo podatke o skupovima pokusâ i otkricâ, tada nam, U POJEDINANOM POKUSU, nije dovoljno postici razinu znacajnosti p<0,05 (ili p<0,01 , ili slicnu), nego je vazno postici mnogo manju vrijednost p.

Vjerojatno ce se gotovo svatko sloziti, da se nul-hipoteza moze odbaciti (uz vrlo mali rizik pogreske) ako se postigne p<10^-9 t.j. p<0,000000001 te da je "gotovo nemoguce" postici tu razinu znacajnosti pri istinitoj nul-hipotezi.
Mozda je dovoljno postici i p<0,000001 (p<10^-6) u pojedinacnom pokusu; ali zapravo bi tek trebalo provjeriti, da li je ta razina znacajnosti zaista dovoljna. (Nije iskljuceno da bi bila dovoljna i neka jos niza razina, mozda oko 0,00001 ili cak oko 0,001 (?), ALI TO BI SE TEK MORALO PROVJERITI na velikim skupovima pokusâ (n) i otkricâ (r) !)

------(B.1) Koji efekt se moze smatrati dovoljno velikim, a koji cemo smatrati zanemarivo malenim?
------(NAPOMENA: s.d. = standardna devijacija ; s.g. = standardna greska)

1. Pretpostavimo da je, u nekoj populaciji bolesnika, raspodjela vrijednosti arterijskog krvnog tlaka priblizno normalna ili bar donekle slicna normalnoj. Raspon vrijednosti tlakova od 6 standardnih devijacija (6 s.d.) mogao bi obuhvacati u nekoj takvoj populaciji, PRETPOSTAVIMO, vrijednosti od 140/95 do 230/125 mmHg (odnosno od 18,67/12,67 do 30,67/16,67 kPa), sa aritmetickom sredinom: 185/110 mmHg. Ako raspon podijelimo sa 6, dobijemo vrijednost jedne stanadardne devijacije (1 s.d.): Za sistolicke tlakove:
1 s.d. = (230-140)/6 = 15 ; za dijastolicke tlakove: 1 s.d. = (125-95)/6 = 5 ; za oba ta tlaka pisati cemo krace: 1 s.d. = 15/5 (Navedene vrijednosti su proizvoljne, ali nisu jako daleko od stvarno mogucih vrijednosti. Na pr., mogu se usporediti sa donekle slicnim vrijednostima iz pokusa: Catipovic-Veselica, 1980.; vidi nize: lit.).

Ako bi neki lijek snizio tlakove cijele te populacije za 0,1 do 0,2 s.d., pojedinom bolesniku snizio bi se tlak samo za 1,5/0,5 do 3/1 mmHg; na pr., tlak od 185/110 mmHg snizio bi se na 182/109 mmHg. Ocito je, da bi taj efekt bio vrlo malen, gotovo zanemariv, te da bolesnik prakticki ne bi imao koristi od toga.
Da bi se srednja vrijednost tlaka snizila na vrijednost blizu normale (recimo, u nasem primjeru, na 140/95 mmHg), trebalo bi ju sniziti za 3 s.d. Ali, u tom slucaju najveca vrijednost raspona (230/125) snizila bi se na 185/110 sto bi moglo biti nedovoljno. Dakle, tek snizenje za 5 do 6 s.d. moglo bi se smatrati dobrim, ili dovoljno velikim, jakim efektom. (Jasno, ako je efekt velik, bolesnici kojima tlak nije jako povisen, morali bi uzimati manje doze lijeka).

Moguce je zamisliti mnogo slicnih primjera; evo jos nekih:
2. Kod neke bolesti mogao bi raspon (6 s.d.) tjelesnih temperatura iznositi otprilike (pretpostavimo) 37,2 do 39,6 stupnjeva C ; 1 s.d. = 0,4 stupnja C ; snizenje za 0,1 do 0,2 s.d. iznosilo bi samo 0,04 do 0,08 stupnja C t.j., na primjer, bolesniku koji ima 38,5 st.C, temperatura bi se snizila na 38,42 st.C (gotovo zanemarivo). Da bi se temperatura od 39,6 snizila bar na 38 stupnjeva C, potreban je, u ovom primjeru, efekt od 4 s.d.
Ili:
3. Ako bi u nekoj populaciji bolesnikâ od secerne bolesti, koji se lijece ambulantno (dakle iskljuceni su najtezi bolesnici), koncentracije glukoze u krvi iznosile izmedju 110 i 250 mg/100ml (pretpostavimo da bi to bio raspon od 6 s.d.) tada je 1 s.d. = 23,3 mg/100ml. Snizenje za 0,2 s.d. - na pr. od 250 na 245,3 - bilo bi gotovo zanemarivo. Da bi se secer u krvi snizio od 250 mg/100ml na normalu, trebao bi efekt od 6 s.d.
Ili:
4. Normalna koncentracija leukocita u krvi je (otprilike) 3000 do 11000/mm3. Dakle, to bi (priblizno) moglo biti 6 s.d. (1 s.d. =1333). Ako kod neke bolesti (na pr. kod akutne upale slijepog crijeva - prema Medicinskoj enciklopediji, I, str.6, Zagreb,1967.) leukocitoza iznosi izmedju 10000 i 15000, te ako pretpostavimo da je to 6 s.d. (1 s.d. = 833), za snizenje vrijednosti 15000 na 11000 potreban je efekt od 4,8 s.d. Itd., itd.

Kod objavljivanja rezultata znanstvenih istrazivanja mnogi se danas zadovoljavaju time, da navedu kako je postignuta razina znacajnosti p<0,05 (ili, na pr., p<0,01), iako su mozda zapravo postigli mnogo visu razinu (t.j. p mnogo manji od 0,01). Odatle se vidi, kako mnogi misle da je dovoljno postici p<0,05 (ili p<0,01) te da eventualno postizanje znatno visih razina nema neku narocitu prednost ni vaznost.

Medjutim, vrlo je vazno postici sto visu razinu znacajnosti. Naime, iz gornjih primjera se vidi da razlika medju populacijama treba biti dovoljno velika, a kod vece razlike medju populacijama lakse ce se postici vrlo visoka razina znacajnosti t.j. vrlo mala vrijednost p, koja moze govoriti u prilog veceg (jaceg) efekta.

Pogledajmo, kakve vrijednosti p proizlaze iz manjih ili veci razlika medju populacijama:
U gornjem primjeru 2 nedovoljno je (gotovo beskorisno) sniziti temperaturu tijela od 39,6 na 39,5 stupnja C, sto iznosi (u tom primjeru) 0,25 s.d. Pa ipak, vec i kod tako malenog efekta lako je postici p<0,05 ako uzmemo nesto vece uzorke. Ako je opseg dvaju uzoraka jednak, na pr. N1 = N2 = N = 98, mozemo ocekivati da ce istoj razlici medju osnovnim populacijama od 0,1 stup.C odnosno 0,25 s.d. odgovarati na uzorcima razlika od oko 1,75 stanadardne greske (krace: 1,75 s.g.), dakle vrijednost p<0,05. (Vidi nize: Vrijednosti od 0,25 s.d. odgovara vrijednost t = 7×0,25 = 1,75 s.g. Buduci da je broj stupnjeva slobode = N1+N2-2 = 2N-2 = 2×98-2 = 194 stupnja slobode, navedenoj vrijednosti t odgovara vrijednost p = 0,04 <0,05).

Ako efekt - t.j. razlika aritmetickih sredina osnovnih populacija - iznosi 0,5 do 1 s.d. (sto je jos uvijek prilicno malen efekt) postignuce razine p<0,05 mozemo ocekivati ako uzmemo dva uzorka sa manjim opsezima: N1 = N2 = N = 32 odnosno 8 (jer je 4×0,5=2 s.g. odnosno 2×1= 2 s.g. - vidi nize!).

Prilicno veliki efekti odgovaraju, u gornjim primjerima, razlikama osnovnih populacija vecim od 3 ili 4 s.d. Pri takvim efektima moze se redovito ocekivati postizanje daleko visih, ili cak ekstremno visokih, razina znacajnosti. Na pr.:
Za efekt od 3 s.d.: ako je N=8, t = 6 s.g., p = 0,00002 ;
--------------- ili: ako je N=32, t =12 s.g., p = 4×10^-18
Za efekt od 4 s.d.: ako je N=8, t = 8 s.g., p = 7×10^-7 ;
-------------- ili: ako je N=32, t = 16 s.g., p = 5×10^-24

Odatle bi trebalo biti jasno, kako nam malo znaci postici p<0,05 ili p<0,01 ako smo uzeli nesto vece uzorke, i koliko su vaznija i vrednija otkrica u kojima se postigne bar razina
p<0,000001 - ili, jos bolje, p< 10^-9 = 0,000000001 .